In today's enterprise, application administrators are increasingly required to be IT generalists with knowledge spanning far beyond the application layer. Applications demand performance and when an application underperforms, we are increasingly looking towards the storage as the potential bottleneck.
For those who are not blessed with a storage background, the learning curve to interpret the numerous storage vendor metrics is steep and the information overload overwhelming. One of those troublesome metrics which is the most difficult to understand (and therefore the most often misunderstood) is storage IOPS. This whitepaper aims to ease the IOPS learning curve by herding together the underlying storage concepts in one guide. Once these are understood, you'll see why IOPS can be critical to the performance of your disk subsystems.
This whitepaper covers the following topics,
- How hard disks work
- Drive response times
- Interpreting drive throughputs
- What IOPS are and why they are so important
- IOPS calculations disk arrays
- Application read/write profiles and effective IOPS
Please note that storage technologies beyond the array interface are not discussed (i.e. SAN, NAS etc).
This whitepaper is based on the article of the same name on Symantec Connect1. Although originally written for enterprise administrators of Symantec's Altiris IT Management Suite, this work is useful background reading for any application administrator.
Table of Contents
Introduction
Disk Performance Basics
Hard Disk Speeds - It's more than just RPM
The Response Time
Disk Transfer Rates; aka the 'Sequential Read'
Zone Bit Recording
Understanding Enterprise Disk Performance
Disk Operations per Second - IOPS
IOPS and Data
IOPS and Partial Stroking
How Many IOPS Do We Need?
IOPS, Disk Arrays & Write Penalties
Normalised Effective IOPS
Optimum drive number for target IOPS
Summary
Further Reading
Footnotes
Introduction
If you are an Altiris Administrator, take it from me that IOPS are important to you. One of Symantec's IT Management Suite (ITMS) underpinning technologies is Microsoft SQL Server and you need to be sure that your SQL server is up to the task. There are many ways to help SQL Server perform well.
Among them are:
- Move both the server OS and the SQL Server application to 64-bit
- Ensure you've got enough RAM chips to load your entire SQL database into memory
- Ensure you've got enough processing power on-box
- Ensure the disk subsystem is up to the task
- Implement database maintenance plans
- Performance monitoring
One of the most difficult items in the above list to get right is ensuring the disk subsystem is up to the task. This is important; you want to be sure that the hardware you are considering is suitable from the outset for the loads you anticipate placing on your SQL Server.
Once your hardware is purchased, you can of course tweak how SQL server utilises the disks it's been given. For example, to reduce contention, we can employ different spindles for the OS, databases and log files. You might even re-align your disk partitions and tune your volume block sizes when formatting.
However, specifying the disk subsystem initially leads to a lot of tricky questions
,
- How fast are these disks really?
- Okay I now know how fast they are.... Is that good?
- Is the disk configuration suitable for my application workload?
Before we can begin to answer these questions, we really need to start at the beginning...
Disk Performance Basics
Disk performance is an interesting topic. Most of us tend to think of this in terms of how many Megabytes per second (MB/s) we can get out of our storage. Our day-to-day tasks like copying files between disks teach us that this MB/s figure is indeed an important benchmark.
It is however vital to understand that these processes belong to a specific class of I/O which we call sequential. For example, when we are reading a file from beginning to end in one continuous stream we are actually executing a sequential read. Likewise, when copying large files the write process to the new drive is called a sequential write.
When we talk about rating a disk subsystem's performance, the sequential read and write operations are only half the story. To see why, let's take a look into the innards of a classic mechanical hard disk.
Hard Disk Speeds - It's more than just RPM...
A hard disk essentially consists of some drive electronics, a spinning platter and a number of read/write heads which can be swung across the disk on an arm. Below I illustrate the essential components of a disk drive. Note I am focusing on the mechanical aspects of the drive as it is these which limit the rate at which we can read data from (and write data to) the drive.

Figure 1: Simplified disk layout (left) and the motion of the head across the tracks (right)
The main items in Figure 1 are,
- The Disk Platter
The platter is the disk within the drive housing upon which our information is recorded. The platter is a hard material (i.e. not floppy!) which is usually either aluminium, glass or a ceramic. This is coated with a magnetic surface to enable the storage of magnetic bits which represent our data. The platter is spun at incredible speeds by the central spindle (up to 150 mph on the fastest disks) which has the effect of presenting a stream of data under the disk head at terrific speeds.
In order to provide a means to locate data on the disk, these platters are formatted with thousands of concentric circles called tracks. Each track is subdivided into sectors which each store 512 bytes of data.
As there is a limit to the density with which vendors can record magnetic information on a platter, manufacturers will often be forced to make disk drives with several platters in order to meet the storage capacities their customers demand.
- The Drive Head
This is the business end of the drive. The heads read and write information bits to and from the magnetic domains that pass beneath it on the platter surface. There are usually two heads per platter which are sited on either side of the disk.
- The Actuator Arm
This is the assembly which holds the heads and ensures (through the actuator) that the heads are positioned over the correct disk track.
When considering disk performance one of the obvious players is the platter spin speed. The drive head will pick up far more data per second from a platter which spins at 1000 Rotations Per Minute (RPM) when compared with one that spins just once per minute. Simply put, the faster the drive spins the more sectors the head can read in any given time period.
Next, the speed with which the arm can be moved between the disk tracks will also come into play. For example, consider the case where the head is hovering over say track 33 of a platter. An I/O request then comes in for some data on track 500. The arm then has to swing the head across 467 tracks in order to reach the track with the requested data. The time it takes for the arm to move that distance will fundamentally limit the number of random I/O requests which can be serviced in any given time. For the purposes of benchmarking, these two mechanical speeds which limit disk I/O are provided in the manufacturer's specification sheets as times;
- Average Latency
This is the time taken for the platter to undergo half a disk rotation. Why half? Well at any one time the data can be either a full disk rotation away from the head, or by luck it might already be right underneath it. The time taken for a half rotation therefore gives us the average time it takes for the platter to spin round enough for the data to be retrieved.
- Average Seek Time
Generally speaking, when the I/O request comes in for a particular piece of data, the head will not be above the correct track on the disk. The arm will need to move so that the head is directed over the correct track where it must then wait for the platter spin to present the target data beneath it. As the data could potentially be anywhere on the platter, the average seek time is time taken for the head to travel half way across the disk.
So, whilst disk RPM is important (as this yields the average latency above) it is only half the story. The seek time also has an important role to play.
The Response Time
Generally speaking, the time taken to service an individual random I/O request will be limited by the combination of the above latency and seek times. Let's take, for example, a fairly mainstream retail laptop hard disk; a Seagate Momentus. From the Seagate website its specifications are,

Returning to our special case of a sequential read, we can see that the time taken to locate the start of our data will be the sum of the average latency and the average seek times. This is because once the head has moved over the disk to the correct track (the seek time) it will still have to wait (on average) for half a platter rotation to locate the data. The total time taken to locate and read the data is called the drive's response time.
I've heard people question this formula on the grounds that these two mechanical motions occur concurrently -the platter is in motion whilst the arm is tracking across the disk. The thinking then is that the response time is whichever is the larger of seek and latency. This thought experiment however has a flaw; once the drive head reaches the correct track, it has no idea what sector is beneath it. The head only starts reading once it reaches the target track and thereafter must use the sector address marks to orient itself (see Figure 2 below). Once it has the address mark, it knows where it is on the platter and therefore how many sector gaps must pass before the target sector arrives.
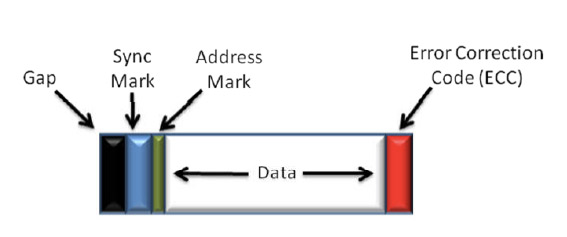
Figure 2: Graphical illustration of a hard disk's sector layout
The result is that when the head arrives at the correct track, we will still have wait on average for half a disk rotation for the correct sector to be presented. The formula which sums seek and latency to provide the drive's response time is therefore correct.
From the drives specification table, the response time for our Seagate Momentus is therefore,
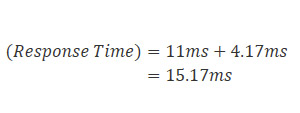
So the drive's response time is a little over 15 thousandths of a second. Well that sounds small, but how does this compare with other drives and in what scenarios will the drive's response time matter to us?
To get an idea of how a drive's response time impacts on disk performance, let's first see how this comes into play in a sequential read operation.
Disk Transfer Rates; aka the 'Sequential Read'
Most disk drive manufacturers report both the response time and a peak transfer rate in their drive specification. The peak transfer rate typically refers to the best case sequential read scenario.
Let's assume the OS has directed the disk to perform a large sequential read operation. After the initial average overhead of 15.17ms to locate the start of the data, the actuator arm need now move only fractionally with each disk rotation to continue the read (assuming the data is contiguous). The rate at which we can read data off the disk is now limited by the platter RPM and how much data the manufacturer can pack into each track.
Well, we know the RPM speed of the platter, but what about the data density on the platter? For that we have to dig into the manufacturers more detailed specification sheet,

This tells us that the number of bits per inch of track is 1,490,000. Let's now use this data to work out how much data the drive could potentially deliver on a sequential read.
Noting this is a 2.5inch drive, the maximum track length is going to be the outer circumference of the drive,

As we have 1490kb per inch data density, this means the maximum amount of data which can be crammed onto a track is about,
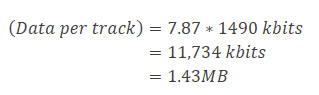
Now a disk spinning at 7200RPM is actually spinning 120 times per second. This means that the total amount of data which can pass under the head in 1 second is a massive 173MB (120 * 1.43MB).
Taking into account that perhaps about 87% of a track is data, this gives a maximum disk throughput of about 150MB/s. This is surprisingly in good agreement with Seagate's own figures (see the second last row in Seagate's spec sheet above).
Note that this calculation is best case -it assumes the data is being sequentially read from the outermost tracks of the disk and that there are no other delays between the head reading the data and the operating system which requested it. As we start populating the drive with data, the tracks get smaller and smaller as we work inwards (don't worry -we'll cover this in Zone Bit Recording below). This means less data per track as you work towards the centre of the platter, and therefore the less data passing under the head in any given time frame.
To see how bad the sequential read rate can get, let's perform the same calculation for the smallest track which has a 1 inch diameter. This gives a worst case sequential read rate of 60MB/s! So when your users report that their computers get progressively slower with time, they might not actually be imagining it. As the disk fills up, retrieving the data from the end of a 2.5inch drive will be 2.5 times slower than retrieving it from the start. For a 3.5 inch desktop hard disk the difference is 3.5 times.
The degradation which comes into play as a disk fills up aside, the conclusion to take away from this section is that a drive's response time does not impact on the sequential read performance. In this scenario, the drives data density and RPM are the important figures to consider.
Before we move onto a scenario where the response time is important, let's look at how drives manage to store more data on their outer tracks than they do on their inner ones.
Zone Bit Recording
As I stated in the above section, the longer outer tracks contain more data than the shorter inner tracks. This might seem obvious, but this has not always been the case. When hard disks were first brought to market, their disk controllers were rather limited. This resulted in a very simple and geometric logic in the way tracks were divided into sectors as shown below. Specifically, each track was divided into a fixed number of sectors over which the data could be recorded. On these disks the number of sectors-per-track was a constant quantity across the platter.
As controllers became more advanced, manufacturers realised that they were finally able to increase the complexity of the platter surface. In particular, they were able to increase the numbers of sectors per track as the track radius increased.
The optimum situation would have been to record on each track as many sectors as possible into its length, but as disks have thousands of tracks this presented a problem - the controller would have to keep a table of all the tracks with their sector counts so it would know exactly what track to move the head to when reading a particular sector. There is also a law of diminishing returns at play if you continue to attempt to fit the maximum number of sectors into each and every track.
A compromise was found. The platter would be divided into a small number of zones. Each zone would be a logical grouping of tracks which had a specific sector-per-track count. This had the advantage of increasing disk capacities by using the outer tracks more effectively. Importantly, this was achieved without introducing a complex lookup mechanism on the controller when it had to figure out where a particular sector was located.

Figure 3: Disk sector layout. Legacy fixed sectors per track (left) and Zone Bit Recording layout (right) with variable sectors per track
Figure 3 above shows an example where the platter surface is divided into 5 zones. Each of these zones contains a large number of tracks (typically thousands), although this is not illustrated in the above pictures for simplicity. This technique is called Zone Bit Recording, or ZBR for short.
On some hard disks, you can see this zoning manifest very clearly if you use a disk benchmarking tool like HD Tune2. This tool tests the disk's sequential read speed working from the outermost track inwards. In the particular case of one of my Maxtor drives, you can see quite clearly that the highest disk transfer rates are obtained on the outer tracks. As the tool moves inwards, we see a sequence of steps as the read head crosses zones possessing a reduced number of sectors per track. In this case we can see that the platter has been divided into 16 zones.

This elegant manifestation of ZBR is sadly hard to find on modern drives -the stairs are generally replaced by a spiky mess. My guess is that other trickery is at play with caches and controller logic which results in so many data bursts as to obscure the ZBR layout.
Understanding Enterprise Disk Performance
Now that we've covered the basics of how hard disks work, we're ready to take a deeper look into disk performance in the enterprise. As we'll see, this means thinking about disk performance in terms of response times instead of the sustained disk throughputs we've considered up to now.
Disk Operations per Second - IOPS
What we have seen in the preceding sections, is that the disk's response time has very little to do with a hard disk's transfer rate. The transfer rate is in fact dominated by the drive's RPM and linear recording density (the maximum number of sectors-per-track.)
This begs the question of exactly when does the response time become important?
To answer this, let's return to where this article started; SQL Servers. The problem with databases is that database I/O is unlikely to be sequential in nature. One query could ask for some data at the top of a table, and the next query could request data from 100,000 rows down. In fact, consecutive queries might even be for different databases hosted on the same server.
If we were to look at the disk level whilst such queries are in action, what we'd see is the head zipping back and forth like mad, apparently moving at random as it tries to read and write data in response to the incoming I/O requests.
In the database scenario, the time it takes for each small I/O request to be serviced is dominated by the time it takes the disk heads to travel to the target location and pick up the data. That is to say, the disk's response time will now dominate our performance. The response time now reflects the time our storage takes to service an I/O request when the request is random and small. If we turn this new benchmark on its head, we can invert this to give the number of Input/Output oPerations per Second (IOPS) our storage provides.
So, for the specific case of our Seagate Drive with a 15.17ms response time, it will take on average 15.17ms to service each I/O. Turning this on its head to give us our IOPS yields (1/ 0.01517) which is 66 IOPS.
Before we take a look and see whether this value is good or bad, I must emphasise that this calculation has not taken into account the process of reading or writing data. An IOPS value calculated in these terms is actually referring to zero-byte file transfers. As ludicrous as this might seem, it does give a good starting point for estimating how many read and write IOPS your storage will deliver as the response time will dominate for small I/O requests.
In order to gauge whether my Seagate Momentus IOPS figure of 66 is any good or not, it would be useful to have a feeling for the IOPS values that different classes of storage provide. Below is an enhancement to a table inspired by Nick Anderson's3 efforts where he grouped various drive types by their RPM and then inverted their response times to give their zero-byte read IOPS,
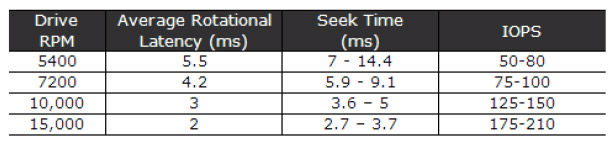
As you can see, my Seagate Momentus actually sits in the 5400RPM IOPS bracket even though it's a 7200RPM drive. Not so surprising as this is actually a laptop drive, and compromises are often made in order to make such mobile devices quieter. In short -your mileage will vary.
IOPS and Data
Our current definition of a drive's IOPS is based on the time it takes a drive to retrieve a zero-sized file. Of immediate concern is what happens to our IOPS values as soon as we want to start retrieving/writing data. In this case, we'll see that both the response time and sequential transfer rates come into play.
To estimate the I/O request time, we need to sum the response time with the time required to read/write our data (noting that a write seek is normally a couple of ms longer than a read seek to give the head more time to settle). The chart below in Figure 4 therefore shows how I'd expect the IOPS to vary as we increase the size of the data block we're requesting from our Seagate Momentus drive.
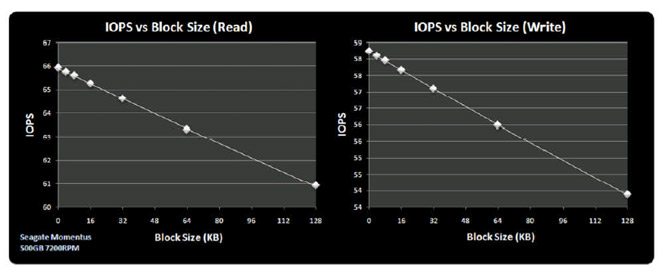
Figure 4: IOPS decline with increasing block size
So our 66 IOPS Seagate drive in a SQL Server scenario (with 64KB block sizes) actually gives us just over 63 IOPS when reading and 56 IOPS when writing.
The emphasis here is that when talking about IOPS (and of course comparing them), it is important to confirm the block sizes being tested and whether we are talking about reading or writing data. This is especially important for drives where the transfer times start playing a more significant role in the total time taken for the IO operation to be serviced.
As real-world IOPS values are detrimentally affected when I/O block sizes are considered (and also of course if we are writing instead of reading), manufacturers will generally quote a best case IOPS. This is taken from the time taken to read the minimum amount from a drive (512 bytes). This essentially yields an IOPS value derived from the drive's response time.
Cynicism aside, this simplified way of looking at IOPS is actually fine for ball-park values. It is worth bearing in mind that these quoted values are always going to be rather optimistic.
IOPS and Partial Stroking
If you recall, our 500GB Seagate Momentus has the following broad specs,
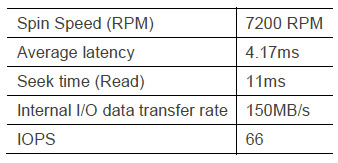
On the IOPS scale, we've already determined that this isn't exactly a performer. If we wanted to use this drive for a SQL database we'd likely be pretty disappointed. Is there anything we can do once we've bought the drive to increase its performance? Oddly, the answer here is yes. Strangely enough we can cheat the stats by being a little clever in our partitioning.
To see how this works, let's partition the Momentus drive so that only the first 100GB is formatted. The rest of the drive, 400GB worth, is now a dead-zone to the heads as they will never go there. This has a very interesting consequence to the drives seek time. The heads are now limited to a small portion of the drives surface, which means the time to traverse from one end of the formatted drive to the other is much smaller than the time it would have taken for the head to cross the entire disk. This reflects rather nicely on the drive's seek time over that 100GB surface, which has an interesting effect on the drive's IOPS.
To get some figures, let's assume that about 4ms of a drive's seek time is taken up with accelerating and decelerating the heads (2ms to accelerate, and 2ms to decelerate). The rest of the drive's seek time can then be said to be attributed to its transit across the platter surface.
By reducing the physical distance the head has to travel to a fifth of the drive's surface, we can expect that the transit time is going to be reduced likewise. This results in a new seek time of (11-4)/5 + 4 = 6.4ms.
In fact, as more data is packed into the outside tracks due to ZBR this would be conservative estimate. If the latter four fifths of the drive were never going to be used, the drive stats would now look as follows,

The potential IOPS for this drive has increased by 50%. In fact, it's pretty much comparable now to a high-end 7200RPM drive! This trick is called partial stroking, and can be quite an effective way to ensure slower RPM drives perform like their big RPM brothers from an IOPS viewpoint. Yes, you do lose capacity, but in terms of cost you can save overall.
To see if this really works, I've used IOMETER to gather a number of response times for my Seagate Momentus using various partition sizes and a 512 byte data transfer.
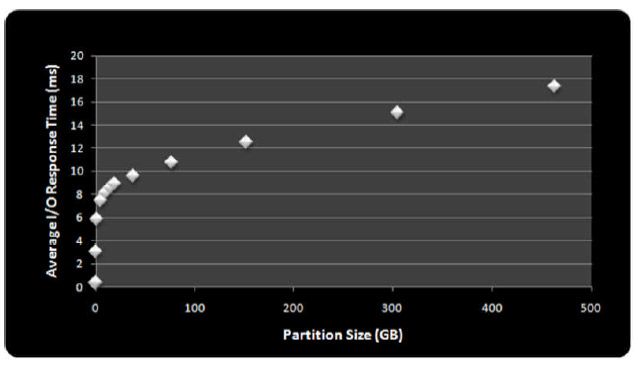
Figure 5: Effect of partial-stroking on I/O response times
In Figure 5 we can see that the back-of-an-envelope calculation wasn't so bad; the average I/O response time here for a 100GB drive worked out to be 11ms and the quick calculation gave about 10.5ms. This agreement however is perhaps more through luck than judgement. I didn't add a head settling time which is required to allow actuator arm vibrations to setting. This omission however was likely absorbed in my slight over-estimation of the arm acceleration and deceleration times.
As a rough calculation however, I imagine this wouldn't be too far off for most drives.
Your mileage will of course vary across drive models, but if for example you are looking at getting a lot of IOPS for a 100GB database, I'd expect that a 1TB 7200RPM Seagate Barracuda with 80 IOPS could be turned into a 120 IOPS drive by partitioning it for such a purpose. This would take the drive into the 10K RPM ballpark on the IOPS scale for less than half the price of a 100GB 10K RPM disk.
Putting this point another way, even though you've lost 90% of your storage in partial-stroking your drive, it's far cheaper from both an IOPS and capacity viewpoint than to upgrade to the more expensive high-performing models.
Please be aware however that partial-stroking is not a mechanism for driving consumer drives into enterprise disk arrays. Enterprise disks are more costly as they are tested and expected to perform around the clock at higher loads, temperatures and vibration levels. Further, they have longer mean time between failures (MBTF) and higher data integrity4.
In summary, this technique of partial stroking a drive, in ensuring that most of a drives surface is a disk head 'dead-zone', can turn a modest desktop hard disk into an IOPS king for its class. And the reason for doing this is not to be petty, or prove a point -it is cost. Drives with large quoted IOPS tend to be rather expensive.
How Many IOPS DoWe Need?
Whilst enhancing our IOPS with drive stroking is interesting, what we're missing at the moment is where in this IOPS guide we should be aiming to target our disk subsystem infrastructure.
To do this, you need to look at some real-world metrics for your target application. As I'm writing this from the viewpoint of an Altiris Administrator, I turn to Symantec's ITSM 7.1 Planning and Implementation Guide. The table below is reproduced from this guide, and shows some interesting figures for a 20,000 node setup where SQL I/O was profiled for an hour at peak time,

The conclusion was that the main SQL Server CMDB database required, on average, 240 write IOPS over this hour window. As we don't want to target our disk subsystem to be working at peak, we'd probably want to aim for a storage system capable of 500 write IOPS.
This IOPS target is simply not achievable through a single mechanical drive, so we must move our thinking to drive arrays in the hope that by aggregating disks we can start multiplying up our IOPS. As we'll see, it is at this point things get murky.....
IOPS, Disk Arrays & Write Penalties
A quick peek under the bonnet of most enterprise servers will reveal a multitude of disks connected to a special disk controller called a RAID controller. If you are not familiar with RAID, there is plenty of good online info available on this topic, and RAID's Wikipedia entry5 isn't a bad place to start.
To summarise, RAID stands for Redundant Array of Independent Disks. This technology answers the need to maintain enterprise data integrity in a world where hard disks have a life expectancy and will someday fail. The RAID controller abstracts the underlying physical drives into a number of logical drives. By building fault-tolerance into the way data is physically distributed, RAID arrays can be built to withstand a number of drive failures before data integrity is compromised.
Over the years, many different RAID schemes have been developed to allow data to be written to a disk array in a fault tolerant fashion. Each scheme is classified and allocated a RAID level. To help in the arguments that follow concerning RAID performance, let's review now some of the more commonly used RAID levels,
- RAID 0
This level carves up the data to be written into blocks (typically 64K) which are then distributed across all the drives in the array. So when writing a 640KB file through a RAID 0 controller with 5 disks, it would first divide the file into 10 x 64KB blocks. It would then write the first 5 blocks to each of the 5 disks simultaneously, and then once that was successful, proceed to write the remaining five blocks in the same way. As data is written in layers across the disk array this technique is called striping, and the block size above is referred to as the array's stripe size. Should a drive fail in RAID 0, the data is lost -there is no redundancy. As the striping concept used here is the basis of other RAID levels which do offer redundancy, it is hard to omit RAID 0 from the official RAID classification.
RAID 0's great benefit is that it offers a much improved I/O performance as all the disks are potentially utilised when reading and writing data.
- RAID 1
This is the simplest to understand RAID configuration. When a block of data is written to a physical disk in this configuration, that write process is exactly duplicated on another disk. For that reason, these drives are often referred to as mirrored pairs. In the event of a drive failure, the array and can continue to operate with no data loss. Read performance is degraded as all reads are from one disk rather than two; thus the array is said to operate in a degraded state.
- RAID 5
This is a fault tolerant version of RAID 0. In this configuration each stripe layer contains a parity block. The storing of a parity block provides the RAID redundancy as should a drive fail, the information the now defunct drive contained can be rebuilt on-the-fly using the rest of the blocks in the stripe layer. This redundancy comes at the cost of losing the equivalent of a single drive's capacity across the RAID 5 array.
Once a drive fails, a single read can potentially require the whole stripe to be read so that the missing drive's information can be rebuilt. Should a further drive fail in the degraded array before the defunct drive is replaced (and rebuilt) the integrity of the array will be lost.
- RAID 6
As RAID 5 above, but now two drives store parity information which means that two drives can be lost before array integrity is compromised. This extra redundancy comes at the cost of losing the equivalent of two drives worth of capacity in the RAID 6 array (whereas in RAID 5 you lose the equivalent of one drive in capacity).
- RAID 10
This is what we refer to as a nested RAID configuration -it is a stripe of mirrors and is as such called RAID 1 + 0 (or RAID 10 for short). In this configuration you have a stripe setup as in RAID 0 above, but now each disk has a mirrored partner to provide redundancy. Protection against drive failure is very good as the likelihood of both drives failing in any mirror simultaneously is low. You can potentially lose up to half of the total drives in the array with this setup (assuming a one disk per mirror failure).
With RAID 10 your array capacity is half the total capacity of your storage.
Below in Figure 6 I show graphically examples of RAID 5 and RAID 10 disk configurations. Here each block is designated by a letter and a number. The letter designates the stripe layer, and the number designates the block index within that stripe layer. Blocks with the letter p index are parity blocks.
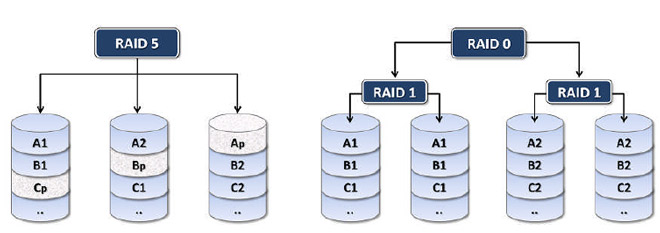
Figure 6: Illustration of two of the major RAID configurations in use today -RAID 5 (left) and RAID 10 (right)
As stated above, one of the great benefits that striping gives is performance.
Let's take again the example of a RAID 0 array consisting of 5 disks. When writing a file, all the data isn't simply written to the first disk. Instead, only the first block will be written to the first disk. The controller directs the second block to the second disk, and so on until all the disks have been written to. If there is still more of the file to write, the controller begins again from disk 1 on a new stripe layer. Using this strategy, you can simultaneously read and write data to a lot of disks, aggregating your read and write performance.
This can powerfully enhance our IOPS. In order to see how IOPS are affected by each RAID configuration, let's now discuss each of the RAID levels in turn and think through what happens for both incoming read and write requests.
- RAID 0
For the cases of both read and write IOPS to the RAID controller, one IOPS will result on the physical disk where the data is located.
- RAID 1
For the case of a read IOPS, the controller will execute one read IOPS on one of the disks in the mirror. For the case of a write IOPS to the controller, there will be two write IOPS executed -one to each disk in the mirror.
- RAID 5
For the case of a read IOPS, the controller does not need to read the parity data -it just directs the read directly to the disk which holds the data in question resulting again in 1 IOPS at the backend. For the case of a disk write we have a problem - we also have to update the parity information in the target stripe layer. The RAID controller must therefore execute two read IOPS (one to read the block we are about to write to, and the other for obtain the parity information for the stripe). We must then calculate the new parity information, and then execute two write IOPS (one to update the parity block and the other to update the data block). One write IOPS therefore results in 4 IOPS at the backend6!
- RAID 6
As above, one read IOPS to the controller will result in one read IOPS at the backend. One write IOPS will now however result in 6 IOPS at the backend to maintain the two parity blocks in each stripe (3 read and 3 write).
- RAID 10
One read IOPS sent to the controller will be directed to the correct stripe and one of the mirrored pair; so again only one write IOPS at the backend. One write IOPS to the controller however will result in two IOPS being executed in the backend to reflect that both drives in the mirrored pair require updating.
What we therefore see when utilising disk arrays is the following,
- For disk reads, the IOPS capacity of the array is the number of disks in the array multiplied by a single drive IOPS. This is because one incoming read I/O results in a single I/O at the backend.
- For disk writes with RAID, the number of IOPS executed at the backend is generally not the same as the number of write IOPS coming into the controller. This results in the total number of effective write IOPS that an array is capable of being generally much less than what you might assume by naively aggregating disk performance.
The number of writes imposed on the backend by one incoming write request is often referred to as the RAID write penalty. Each RAID level suffer from a different write penalty as described above, though for easier reference the table below is useful,
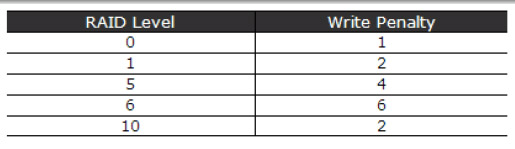
This is interesting; applications which issue random I/O will see a different IOPS response depending on whether it's a read or write request. The more write biased the distribution of application I/O is, the heavier the impact on the resultant IOPS. Knowing this fraction of writes vs reads is therefore critical in configuring your storage. Application vendors will generally provide this data for you from their live environment profiling.
Knowing the write penalty each RAID level suffers from, we can calculate the effective IOPS of an array using the following equation,
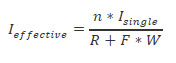
where n is the number of disks in the array, Isingle is a single drive's IOPS, R is the fraction of reads taken from disk profiling, W is the fraction of writes taken from disk profiling, and F is the write penalty (or RAID Factor).
This equation is a critical storage array design tool. It should also be nothing less than your first port of call when establishing any storage array's fundamental response to random I/O patterns.
Normalised Effective IOPS
As vendors will typically cite their array IOPS at the maximum (the number of drives multiplied by the IOPS of single drive), you can write the above equation a different way,
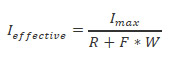
To give the equation a little grounding, it can be useful to map a metric we'll call the normalised effective IOPS,
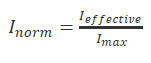
This can be useful as a multiplying factor to extract a real-world IOPS figure from your vendor's quoted maximum IOPS.
The chart below in Figure 7 shows how the normalised effective IOPS of various RAID configurations vary with an application's read/ write IOPS fraction. This allows you to extract an effective IOPS from an array simply by selecting your RAID level and application write profile.
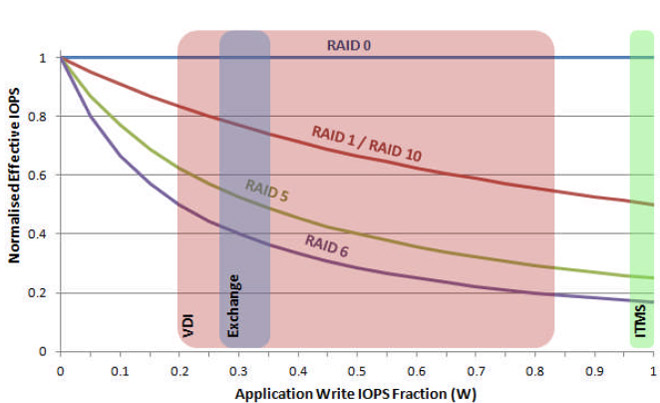
Figure 7: Variation of normalised effective IOPS with application profiling write fraction
As a concrete example, imagine a storage solution consisting of 25 15K SAS drives. Each SAS drive has 200 IOPS and the array is therefore quoted as having a maximum 5000 IOPS.
Let's now consider an application which is profiled as having 100% reads and 0% writes. At 0% write, all RAID types naturally have converged to give a normalised IOPS value of 1; the write penalty is unseen. The maximum quoted array IOPS will therefore likely reflect the reality of what your application will be served and will be independent of the RAID level you choose.
However, if we consider applications with a write element to their I/O profiles, we move to the right of the graph, along the RAID curves, and our effective IOPS plummet. To illustrate, consider an application with a 50/50 read/write profile. Looking at the intersection of the RAID lines with the 50% write value on the graph yields the following normalised and effective IOPS values;
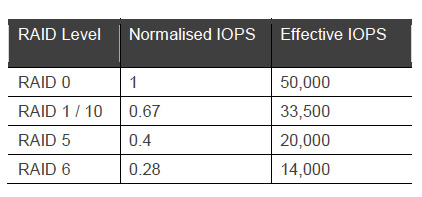
This is significant. Even through the array is quoted at 5000 IOPS, our application will in reality never see this once we implement a RAID with redundancy.
It's worth for a moment considering the storage implications too. The mirrored RAID levels suffer the least IOPS loss, but at the cost of halving the available storage. Conversely, introducing redundancy through parity, whilst more effective in terms of storage capacity, results in the greatest IOPS loss. This is the storage conundrum; the balancing of optimum capacity and IOPS.
In Figure 7, I've highlighted three zones to illustrate where different applications might exist on the graph. For example, the red zone is for VDI (Virtual Desktop Infrastructure) where quoted read/write profiles vary hugely. Next we have a blue zone for Microsoft Exchange SQL Server where the random I/O pattern is expected to be around 66% read and 33% write. The final zone, highlighted in green, is for the Symantec ITMS SQL database where we expected a predominantly write biased profile.
In the particular case of the application demanding 100% write IOPS, we've seen that the vendor's quoted maximum IOPS will hugely over-estimate the real-world array performance. Just how much degradation you'll see on account of the dwindling normalised effective IOPS multiplier of course clearly depends on the RAID level you decide to implement.
Optimum drive number for target IOPS
If we know in advance the number of IOPS we need from our storage array we can rearrange the effective IOPS equation to give us the minimum number of drives we'll need to meet the IOPS requirement,
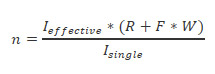
Returning to the specific application case of Altiris ITMS, we recall that the SQL Server requirement is that it should be capable of 500 write IOPS. If we assume a storage solution of 10K SAS drives, capable of 120 IOPS a piece, how many disks would we need to meet this write IOPS requirement?
The table below summarises the results.
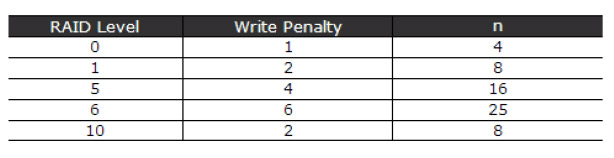
What we see here is a huge variation in the number of drives required depending on the RAID level, which has a direct implication on the cost of your storage array. This once again highlights that your choice of RAID configuration is very, very important if storage IOPS is important to you.
As vendors are well aware of the performance hit incurred for write IOPS with respect to RAID configurations, they will try to cache writes when possible. The idea is that by committing to cache, they can perform a disk commit during a more favourable window. As a result, in real-world scenarios, controllers often perform better than you'd anticipate from data above. However, once these arrays become highly utilised the favourable windows dwindle making the write cache less effective. At this point, the array performance edges back towards the IOPS values anticipated for the RAID configuration and application profile.
Summary
The primary objective of this whitepaper is to get you thinking more about disk performance rather than disk capacity when planning your application storage requirements. Specifically, you need understand from your application vendor whether IOPS are likely to be a bottleneck in your implementation.
The main points to take away from this article are,
- The important measure for sequential I/O is disk throughput
- The important measure for random I/O is IOPS
- Choosing your storage RAID level is critical when considering your IOPS performance.
- The effective IOPS your application sees will be highly dependent on your application's distribution of random disk reads and writes (the read/write fraction)
- Get involved with your server/storage team when it comes to planning your storage
So, when designing your storage, please consider the applications that use it. You'll need to look at their IOPS requirements as well as the anticipated array capacity (allowing for growth in both).
Please remember that this whitepaper is a starter on the disk performance journey. As such, this document should not be considered in isolation when benchmarking and specifying system configuration.
Further Reading
http://www.pcguide.com/ref/hdd - This is a great reference and includes everything you'd ever want to know about how hard disks work
http://www.zdnet.com/blog/ou/how-higher-rpm-hard-drives-rip-you-off/322 - the blog entry which got me interested in drive stroking
http://www.seagate.com/staticfiles/support/disc/manuals/notebook/momentus/XT/100610268b.pdf - the Seagate Momentus specification sheet
http://vmtoday.com/2009/12/storage-basics-part-i-intro/ - A nice series of articles by Joshua Townsend on storage
http://www.seagate.com/docs/pdf/whitepaper/tp613_transition_to_4k_sectors.pdf -an interesting Seagate whitepaper on the transition from 512 Byte sectors to 4K sectors.
http://www.techrepublic.com/blog/datacenter/calculate-iops-in-a-storage-array/2182 -Scot Lowe's great TechRepublic article on IOPS and storage arrays
http://oss.oracle.com/~mkp/docs/ls-2009-petersen.pdf -Martin Peterson's paper on I/O topology Symantec HOWTO10723 --SQL Server 2005 and 2008 Implementation Best Practices and Optimization - A very instructive Symantec knowledge base article on improving SQL Server performance
Footnotes
- http://www.symantec.com/connect/articles/getting-hang-iops
- http://www.hdtune.com/
- http://www.cmdln.org/2010/04/22/analyzing-io-performance-in-linux/
- http://download.intel.com/support/motherboards/server/sb/enterprise_class_versus_desktop_class_hard_drives_.pdf
- http://en.wikipedia.org/wiki/RAID
- Please note that in serial write scenarios, the RAID controller may be able to perform a full stripe write. This has the I/O benefit of the controller not having to read the stripe data in advance.